Solution

Because this problem explicitly involves forces, conservation of energy alone can't be sufficient to solve this problem. But we've seen from the pendulum example above it is extremely powerful and so we'll use it in addition to Newton's laws.

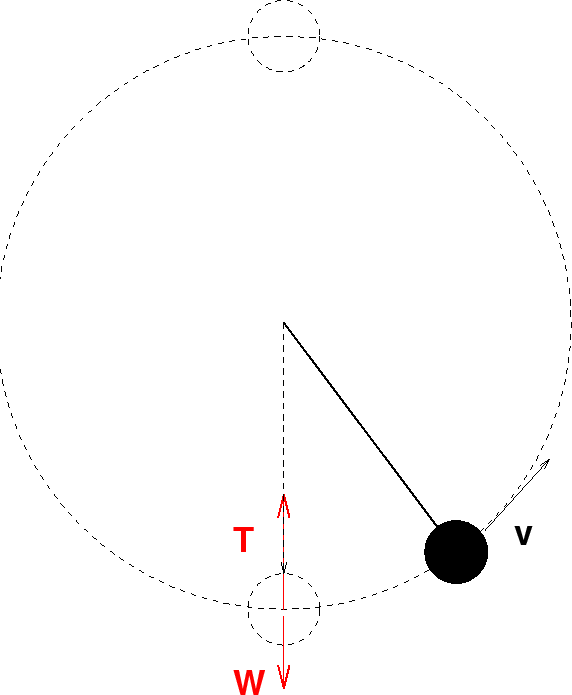
So how about Newton's laws applied to the ball at the bottom? Well ${\bf F}_{net} ~=~ m{\bf a}$. What's the acceleration? It's not zero because the ball is traveling around in a circle. We know that it points up and has a magnitude of $v^2/R$. What's the net force? The tension points up, but the weight $mg$ goes down so we have

$$T_{bottom} -mg ~=~ mv_b^2/R$$ (1.21)

where $v_b$ is the speed at the bottom.

The tension at the top is similar but we have to realize though that the acceleration and the tension are now both pointing in the opposite directions what what they were on the bottom, so

$$-T_{top} -mg ~=~ -mv_t^2/R$$ (1.22)

where $v_t$ is the speed at the top.

We were asked for the difference between these tensions so adding these equations, we have

$$T_{bottom} - T_{top} -2mg ~=~ m(v_b^2-v_t^2)/R$$ (1.23)

So this is all we'll use of Newton's laws. Now we need to figure out $m(v_b^2-v_t^2)$, which looks awfully closely related to kinetic energy, so now we'll use conservation of energy to figure it out.

Let's define our coordinate system so that $y ~=~ 0$ at the bottom of the circle. Then the energy at the bottom is $K+U ~=~ {1\over 2}mv_b^2$, and the energy at the top is $K+U ~=~ {1\over 2}mv_t^2 +mg2R$. Equating these two energies, we see that

$${1\over 2}m (v_b^2 -v_t^2) ~=~ 2mgR$$ (1.24)

Using this is eq. 1.23 we have

$$T_{bottom} - T_{top} ~=~ 2mg + 4mg ~=~ 6mg$$ (1.25)

which is what we wanted to show.

Again this problem would be possible, but very hard to solve using Newton's laws alone.