Work with variable forces in 3d

Let's repeat the same logic we did in one dimension. We'll think about a force now that's a function of position in three dimensions. What's an example of this? Well the earth going round the sun. The force of the sun on the earth depends on where the earth is located. Another example is a bungey cord with one end anchored down. The force exerted by the other end depends on how far away it is from the anchor.

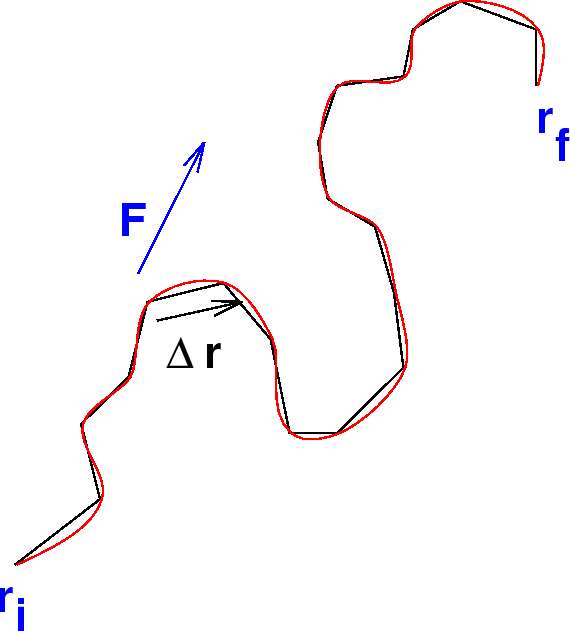
Following the same logic, we'd think about moving an object along some three dimensional path as shown below.

To get the total work, we'll approximate the smooth red path by the black line segments as shown. Then we'll approximate the force as being constant on a particular line segment. The reason for doing this, is that we know how to calculate the work done by a constant force in going in a straight line. For one of these line segments its just ${\bf F}\cdot \Delta {\bf r}$. Now we want to sum over all these different line segments. You could write it as

$$W ~ \approx ~ \sum {\bf F}\cdot \Delta r$$ (1.14)

Now we'll take the same old calculus limit as before, but this time we'll get what's known as a line integral

$$W ~ =~ \int_{{\bf r}_i}^{{\bf r}_f} {\bf F}\cdot d{\bf r}$$ (1.15)

The meaning of the line integral is just as we described. You some up all the incremental work going along this path, taking infinitesimal steps as you go along it.