Newton's Laws

So now what we want to do is ask how do the forces acting on an object relate to it's motion? Well that was a real tricky business for a few millennia. We'll just say what the answer is without too much justification, the justification being that it works real real well. But bear in mind that it took the human race a long time to figure this out. So ones first guess is that the bigger the force, the bigger the velocity. That's not quite right. You see in outer space, you can have a spaceship going at very high velocity relative to the earth, but hardly any forces acting on it. The force doesn't relate directly to the velocity, but to its derivative: the acceleration.

Smartass

But wait a second! You think you can find a law relating the force acting on an object to its acceleration? That's bull! I can show you two cases where you have the same forces acting on the objects, but their motion is different.

Sir Isaac

Oh yes, doth though really think so? Do thee realize there is more brains in my little finger than you're entire hand. Actually I'm not really too sure about brains. After all I'm the inventor of mechanics, not neurophysiology. So go on, you scaliwag.

Smartass

Yes well my example, stupid, is what happens if you drop a glass of coke from inside a car turning a corner, as opposed to what happens to the same coke inside the cinema. While the coke is in free fall, it only feels the force of gravity. And it's the same force in both cases right? Well in the cinema, it ends up on your own lap, whereas in the car it ends up on someone elses. Clearly a different outcome, but the force is the same.

Sir Isaac

Coke? Cars? Cinemas? I'm not suppose to know about that, but anyway, how pretentious of you to say cinema. Don't you really want to say movie theater? Your from the US after all.

Smartass

Stick to the point. If there's a law relating force to acceleration, I can't see how it's going to work out. You get two different types of behavior from the same forces.

Sir Isaac

Well suppose your car hadn't been turning a corner, but just going straight a constant velocity?

Smartass

Well then the outcomes would now be the same, but you never said anything about having to go at a constant velocity. A law is a law. You can't start adding extra stipulations like this just cause you're in a bit of pickle. Next thing you'll be telling me that the car has to be a Chevy and it can't be a pepsi.

Sir Isaac

Quite the contrary. I only have to stipulate three laws and what you've hit on is my first law. It says: I hereby do decree that my next two laws are only true in what'll be called an inertial reference frame. (Actually Albert Einstein would have used that terminology). In such a reference frame, if no forces are acting on an object, it'll just move at constant velocity.

Smartass

Constant velocity? That seems pretty stupid to me! Do you know anything that moves at just a constant velocity? Things will all eventually slow down if they're not being pushed. I mean if I give my Bill Clinton blow-up-doll a push on a table, it might move for a while, but eventually it'll come to rest.

Sir Isaac

Haven't ever heard of friction? That's a force. The same Bill Clinton blow-up-doll moving around in outer space will move at a constant velocity.

Smartass

But when have you seen a Bill Clinton blow-up-doll in outer space Izzy for crying out loud? Get real, I mean you're really in cloud coo coo land. You want laws that work on the ground.

Sir Isaac

I'm beginning to find this conversation exceedingly tiresome. The laws of physics are better understood on the space shuttle where you don't have gas all around you, unless you've just had NASA's 3 bean salad (Groan Groan). Those little gas atoms complicate everything in an extremely uncool way. Once thou hast understood my three laws, we can start discussing mundane matters of why things don't keep moving, such as the force of friction, air resistance, and check out lines at the supermarket on Saturdays.

OK, so now how about Newton's two other laws? The second law says that the acceleration of an object is proportional to the net force acting on an object. Proportional? That's not very precise. Well it's proportional because it depends on the mass of the object.

The more massive, the less it responds. The idea of mass is really related to this second law. If you have two objects that are acted on by the same force, say that one accelerates at 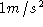and the second one at 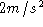, then the first one is twice the mass of the second. In more general, one could say that the ratio of their accelerations in inversely proportional to the ratio of their masses. So there is this idea about mass. Using this idea then we can write down Newton's second law:

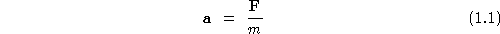
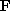Where is the acceleration of the object, the net force acting on the object, and m is its mass.

Now how about the third law? It says that forces always come in pairs. They are equal in magnitude but opposite in direction. Let's illustrate this with the banana split and the earth. While the banana split is accelerating towards the earth, it has a force acting on it due to the earth's gravitational field. Call this 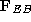. There is another force however that isn't so obvious. Its the force the banana split exerts on the earth. Call this . 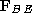Well the earth is much bigger so it's natural to think that the first force is much bigger than the second, but no! The two forces have same magnitude and opposite direction, in equations, .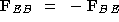

Well another example of force pairs are those between your feet and the ground. As I said earlier, there's a force the ground exerts on your feet. There is another force due to your feet that act on the ground. These two forces are about to have a conversation:

F feet on ground

Don't find it a bit boring just exerting a forces the whole day?

F ground on feet

I don't find it the least bit boring, after all that's why I'm here. I'm a force.

F feet on ground

Well so am I but I think that we tend to behave quite opposite. Why do you think that is?

F ground on feet

Well its Newton's third law. We're suppose to have equal magnitude but opposite direction.

F feet on ground

Well I don't think it's Newton's third law at all.

F ground on feet

Oh, look whose talking! You know more about forces than Newton!

F feet on ground

Well I'm a force after all, so shouldn't I know more?

F ground on feet

So am I but I think you're don't know anything. If it's not Newton's third law that make us equal magnitudes but opposite directions, then what is it?

F feet on ground

My reasoning is this. Newton's second law says that if the acceleration is zero, then so is the net force. Well to make the net force zero, we should be equal in magnitude and opposite in direction.

F ground on feet

Well let me gather my thoughts for a moment. No you're wrong. What if the ground was moving, say in an earthquake, or if we were in an elevator. Then the acceleration would not be zero. So what would you say then.

F feet on ground

Our magnitudes should differ in that case.

F ground on feet

No they don't. See there's an earthquake right now. No difference at all. So you're wrong again. And that brings me to a related paradox. The camel that won't giddy up because he says that according to Sir Isaac, he can't move. You see the third law says that for every force there is an opposite one with equal magnitude and opposite direction.

F feet on ground

Yes like you and me. So what?

F ground on feet

Well then the total force must be zero so the acceleration of the camel is zero. Therefore a resting camel stays resting.

F feet on ground

Well I can't see the resolution to this one either.

F ground on feet

Of course not, the answer will explain the fallacy of your argument of why we should have the same accelerations.

F feet on ground

So don't keep me in suspense. What's the fallacy?

F ground on feet

The point is that you and me are acting on two different objects. Newton's second law is the net force acting on the same object. So the feet get me, and the ground gets you. We're acting on two different objects and aren't added together at all.

F feet on ground

Say, that makes sense, but I've got an uneasy feeling about this conversation. I mean, how can we be talking at all? All we are are forces, a magnitude and a direction. Don't you need more than that to think?

F ground on feet

Yes, well in order to be able to do sophisticated reasoning we need to be of a minimum complexity. This sort of thing is related to the notion of Turing machine. We are definitely below that complexity.

F feet on ground

So this conversation is really taking place is it?

F ground on feet

No. I guess we should stop talking then.