Next: other systems Up: Simple Harmonic Motion Previous: Imaginary numbers aren't so
Let's figure out what the kinetic and potential energy is during different
phases of an oscillation. The kinetic energy is
![]() , and we
calculated
, and we
calculated ![]() in 1.7. Using that, and also that
in 1.7. Using that, and also that
![]() ,
,
| (1.36) |
The potential energy is
![]() so
so
| (1.37) |
If we calculate ![]() we get
we get
 |
(1.38) | ||
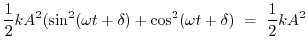 |
(1.39) |
Here we plot the both the position as a function of time and underneath that, kinetic and potential energy.
See how the energy shifts form, constantly transforming between kinetic and
potential. For example, Initially all the energy is potential, as the mass
is at it's maximum and the velocity is zero. A quarter of the way through
a cycle, all that potential energy has gone to kinetic as the mass passes
through ![]() . Then it starts slowing down as it heads over to negative
. Then it starts slowing down as it heads over to negative
![]() . Eventually at half a cycle, the spring is maximally compressed
and the energy is all potential again.
. Eventually at half a cycle, the spring is maximally compressed
and the energy is all potential again.
josh 2010-01-05