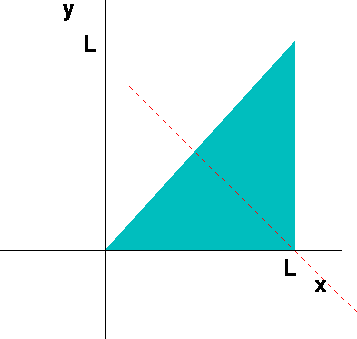
So we break up the integration into x and y directions.
By symmetry if we get the answer along the x direction, we can easily figure out what it should be along the y direction. In fact it's intuitively clear that the center of mass lies along a line that goes 45 degrees through the right angled corner, as seen below.
{
So let's get the answer for the x direction.
This means the following. We've divided up the integration into vertical strips. We first integrate over y to find out the answer in one strip. Then we integrate over all x to find the final answer of all integrated over all strips.
{
Doing the top and bottom integrals over dy we have
By complete chance, we just did this calculation for the
one dimensional rod, see 1.27.
The answer was 
. So we know the center of mass in the
x direction. The y-direction is almost the same problem, but slightly
different. In the x-direction, the triangle is becoming thicker
with increasing x, in the y direction it is becoming thinner with
increasing y. So it makes sense just to say the center of mass in
the y direction is
from the thinner end. This means its
from the thicker end, so it has coordinate
.
{
Tricks like these save you from having to do tedious calculations. You can do the integral the more complicated way if you're unsure that this reasoning is correct.
