Wheels are a marvelous invention that allow us to zip around a lot faster than we would normally with our own two legs. Whatever cave-creature that invented the wheel should certainly be given the Nobel prize. On the other hand, they did choose a pretty stupid spelling for their invention.
A lot of mechanics problems involve wheels. There interesting because they couple translational motion with rotational motion. If a wheel is rolling with a velocity v, what is it's angular velocity? We can compute that by considereing the figure below.
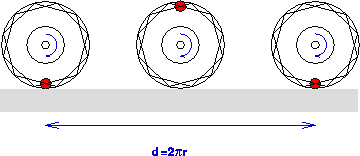
The red dot marks a fixed spot on the rim of the wheel. In the first
snapshot, the red dot is next to the ground. In the second, it has
rotated 180 degrees and is now at the top. Finally at time T, it's back
at the ground again. The wheel has done one revolution and in the
same time, the center of the wheel has gone the wheel's circumference
, where r is the radius of the wheel. Now the angular
velocity 
. That is, it has done 
radians
in the time it takes to make one revolution, T. So the velocity
Imagaine that! It's our old friend 
. But this means something
quite different here. The v here is the center of mass velocity of the
wheel. Our old friend refers to a different v, the velocity of the rim
of the wheel when the center isn't moving. OK, so what do we make out
of all of this? We can think of rolling as combining a pure translation
of the wheel at center of mass velocity 
with rotational
motion with angular velocity 
. This then tells us what the
speed of the wheel is at various places on it's rim. For example, at the
top of the wheel, we add to the velocity due
to rotational motion 
. This gives 
.
At the bottom of the wheel, right next to the ground, these two effects
cancell, and so the velocity of the wheel at the ground is zero!
This makes sense, because if it where different from zero, the wheel
would be sliding along the ground, which we are not allowing.
The following is a sketch of the velocity vectors for several
points along the rim of the wheel.
Notice that it is identical to the velocity if the wheel was pivoted at the bottom. So instantaneeously a rolling wheel looks as if it's pivoted.
