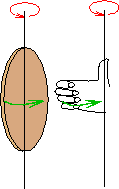
Let's think about angular velocity. We could make it a vector by giving a direction. That seems a bit tough at first sight. There seem to be a lot of directions to the velocity of a rotating coin. Different parts are going in totally different directions. But suppose we wanted to uniquely define a direction so that everyone could tell what axis the object was rotating for this one direction. What would we use? Well the axis of course! Like take the earth. It rotates around an axis and knowing that, you uniquely have the direction of rotation. All except, you don't know if it's spinning clockwise or counter-clockwise (as seen looking down from the north pole). Well that's OK because though we have the axis, we don't yet have a direction for the axis. It could be an arrow pointing up, or one pointing down. So we define something called the right hand rule that says that if you take your right hand and have your fingers follow the direction of rotation, your thumb will define the direction of the angular velocity vector.
So to make a respectable vector out of the angular velocity, we say we take it with the magnitude as defined before, and direction given by the axis of rotation and the right hand rule.