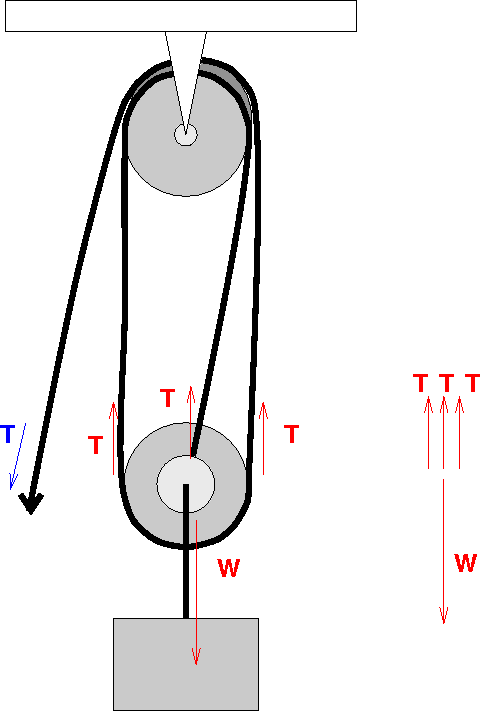
Another rather important example is that of pulleys that have been used for thousands of years to lift up large weights. The figure below illustrates a pulley.
How hard do you have to pull to keep the weight hanging, or moving up at a constant velocity?
Assuming that the ropes can slide freely over the wheels, the tension along the rope is the same everywhere. So we have the free body diagram illustrated above on the right. We've also assumed that the weight of the pulley and rope is negligible compared to the weight that's hanging.
If the system is not accelerating, then the sum of the forces
in this free body diagram must add up to zero. That says that
, or the tension 
. So you have to supply
a tension of a third the weight of the object to keep it hanging.
Of course if you wrapped the rope around the wheels more times, it'd be even easier to lift the weight. The problem is that you'd have to pull a lot more rope that way than if you wrapped it just a few times. We'll see later why this has to be in order to conserve energy.
