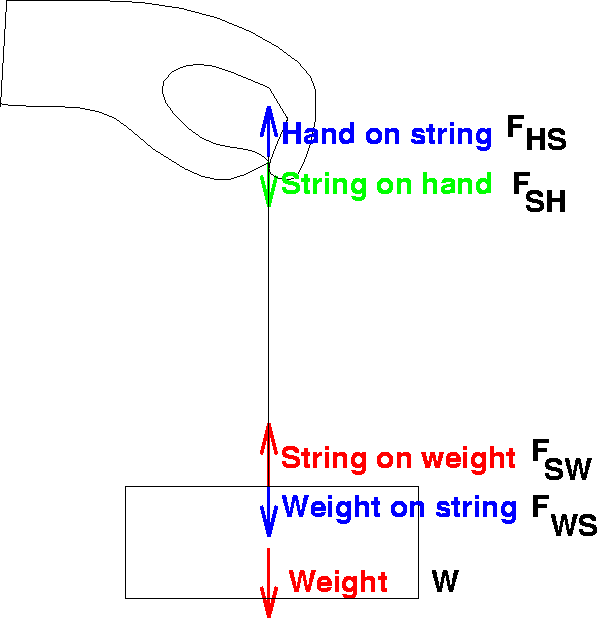
Now a lot of problems will discuss will involve ropes and strings. Most of the time, we'll assume that they are massless, or more precisely, that the mass of a string is much smaller than the other masses in the problem. As you know from everyday life, if you grab a weight by a string, you feel the full force of weight transmitted through the string. This is illustrated in the figure below.
Here we have a person holding a string that's attached to a weight. The different colored arrows correspond to the forces acting on different objects. The red arrows correspond to the forces acting on the weight. The blue correspond to the forces acting on the string, and the green arrow, the force acting on the hand.
We want to figure out what is the force acting on the hand.
So we consider each object separately. Call the force
of the exerted by gravity on the weight 
.
Call the force of the weight on the string 
. These
names are listed in the figure.
Then
It equals zero because the weight isn't moving so the acceleration is zero.
Now lets look at the equation for the string, which involves the blue forces:
This equals zero even if the acceleration is not zero. This is because we're assuming the mass of the string is zero. The force exerted by the string on the weight, is called the ``tension''.
Now let's apply Newton's third law. We know that forces come in pairs
so that 
, and 
.
Putting this all together, we quickly see that 
.
As you can see from the above equation, the tension transmits the force of gravity that acts on the weight, to a force acting on the hand. This is a general feature of massless strings, and is true even if there is acceleration. That is the magnitude of the force exerted at one end of a massless rope is the same as on the other side, which can be seen from eq. 1.5.
