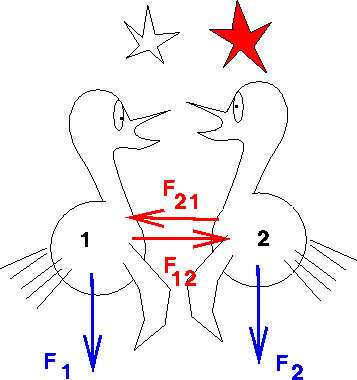
Now we have to distinguish between two different kinds of forces, internal and external. Think about two booby birds as being our system. Suppose they fly into each other.
There are forces between
the birds when they hit, the force that 1 exerts on
2 and the force that 2 exerts on 1, 
and 
respectively.
These are internal to the
booby bird system. But also both birdies are acted
on by the force of gravity, so the the weight of each bird,
and 
is an external force, namely the earth acting on each bird.
The total force acting on
booby 1 is the sum of the internal, 
, and the
external, 
, forces, 
.
Similarly for the second bird, 
.
Now let's calculate the net external force on these boobies.
It's 
.
This is the net external force
acting on the system. Remember the birds have forces between
each other too, and . But I didn't
include these. However even if I did the answer would
be unchanged. That's because of Newton's third law the internal
forces are equal and opposite, so they cancel.
(Of course the
forces don't cancel for each booby, they definitely feel the
force of their brethren bird. But and
act on different objects, not on the same bird.)
But we just learned that
and
So combining these we see that
By using summation notation you can easily see how to extend this result to N particles, so that
Good. Now we see that the rate of change of total momentum is the net (external) force acting on the system. This momentum thing is starting to look more useful!
