Suppose you have a bear that is running about inside a moving train. You're trapped
on board the train watching the bear quite intently. You monitor the bear
in from a coordinate system on the train. Call the position vector as seen
from this coordinate system 
, that is the coordinates of the
bear relative to the train. Call the coordinates of the train seen from
a coordinate system on the ground 
. A person on the ground
wants to know what are the bear's coordinates seen in the reference frame
on the ground, 
. How can we determine what this is?
We can see all this pictorially in the figure below.
Click here to see the full figure
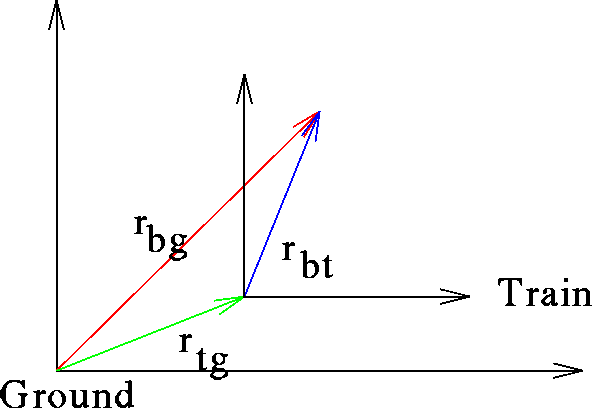
From the figure we see the following relation between the above vectors:
Differentiating the above formula with respect to time, we see the velocities are related the same way:
So to get the velocity of the bear as seen from the ground, you add up the velocity of the train to the velocity of the bear relative to the train.
Differentiating again, one sees that the relation between the accelerations is
So if the train is traveling at constant velocity, the acceleration of train is zero. That means the acceleration of the bear as seen from the ground and as seen from the train are identical.
