This section is similar to the calculation of the center of mass for a continuous body, so I won't repeat all the boring steps. You can easily fill those in if you understand how to do multiple integration and you understand how to get the formula for the center of mass of a continuous body.
If you have a continuous object with a density that varies
with position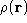 
, then you can write the formula
for the moment of inertia as
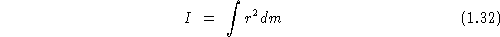
A less mysterious way of writing this is
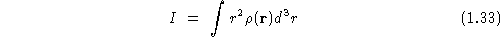
Let's examine what the formula says.
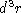and sum up the moment of inertia dI of all the cubes 
.
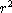where r is the distance away from the axis of
rotation. Don't confuse this r with the distance away from some point.
It's the distance away from the axis of rotation. That is the shortest
distance between the point and the axis of rotation, just like in the last
example. So we have 
.
.
Let's now to some examples.